この問題が解けたらIQ130以上!?モンティホール問題とその解説

論理的思考力を鍛えるためには、日々深く考えることが大事だと言われます。
社会で生き残るためには論理的思考力が必要ですし、論理的思考力が強いと、仕事でも強い力を発揮してくれます。
今回は、HSPの方をはじめとして、多くの人に紹介したい、深く考えさせてくれる問題とその解説を紹介したいと思います。
もしかしたら、この問題が解ければ、あなたはIQ130以上の天才かもしれません…!!
この問題が解けたらIQ130以上!?モンティホール問題

では早速、問題を紹介していきましょう。
ここに、A・B・Cの3つの箱があります。
この3つの箱のうち1つだけ、当たりが入っています。
あなたは、この1/3の確率を当てることができれば、100万円がもらえます…絶対に外せませんね。
今日のラッキーナンバーは「1」だったあなたは、Aの箱を選ぶことにしました。
この緊張した瞬間は、テレビ番組に放送されています。
そのため、司会者は番組を盛り上げるため、こう言いました。
「それでは、他の箱を一つ開けちゃいましょう。では、Bを開けます!」
司会者がBを開けました。そのため、残る箱はあなたが選んだAの箱とまだ司会者が開けていないCの箱だけ残っています。
意地悪な司会者は更にこう付け加えました。
「今であれば、AからCの箱に選択を変えることもできます。あなたはどうしますか?」
この緊張した空気感…、あなたは選択を変えた方が良いのでしょうか?
答えは、画像の下に記載しています。
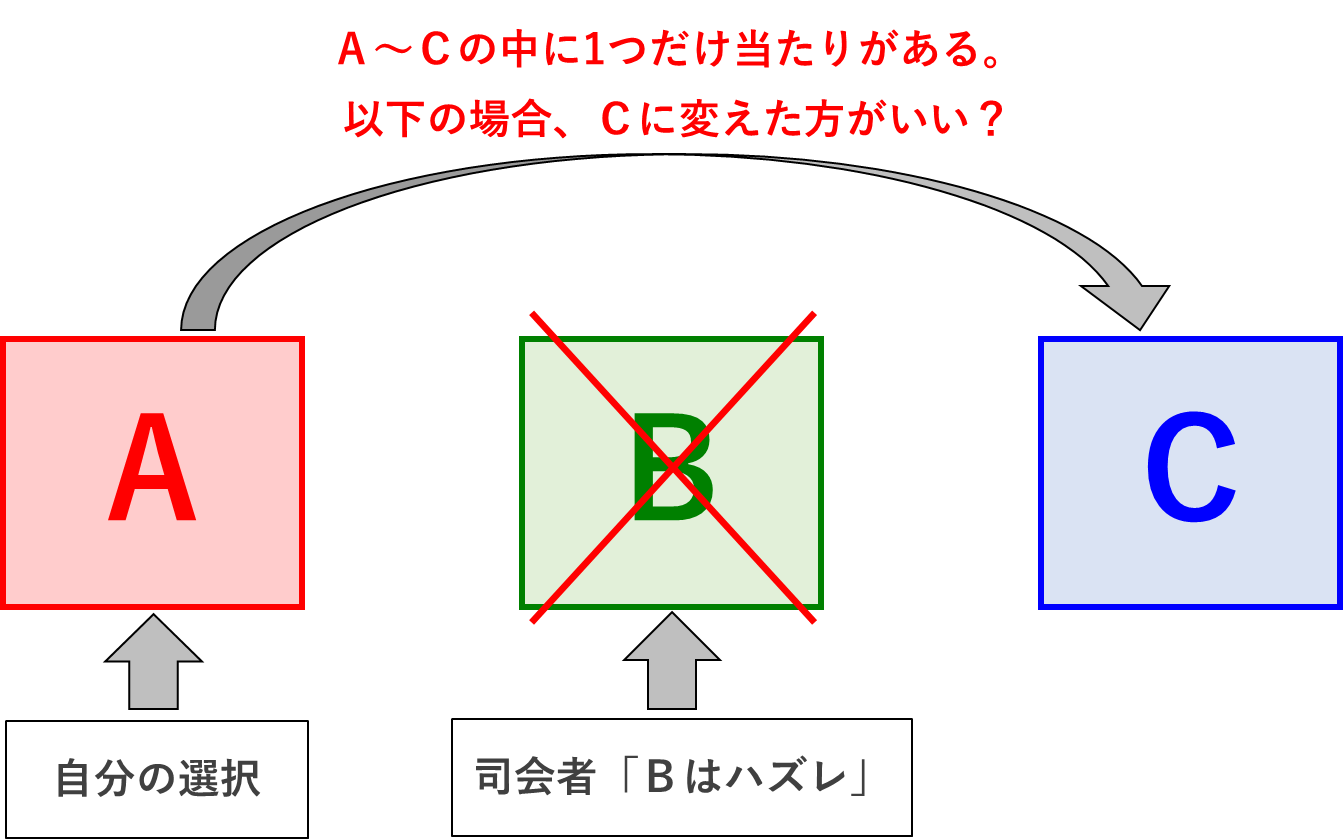
これは、既に知っている人は知っていると思いますが、有名なモンティホール問題といいます。
なぜ有名かというと、直感的な答えと論理的な答えにズレが生じる人が多いため、話題になったからです。
恐らく、この問題を初めて見た多くの人が、「Aのままでも、Cに変えても確率は変わらない。」と思ったのではないでしょうか?
世界一IQが高い人間(IQ228)と呼ばれる、アメリカ人のマリリン・ボス・サバント氏にこの問題がよせられた際、米紙にてこう答えました。
「Cに変えた方が、2倍当たる確率が高い」と。
そんな馬鹿な…と思う方もいるかも知れません。
実際に、彼女の答えには大きな反響があり、全米を巻き込む大議論が生まれました。
でも、シミュレーターで試行を重ねた結果においても、彼女の答えが正しいことが証明されています。
それでは、その理由を解説していきたいと思います。
…と、その前に、なぜ感覚的には、「Aのままでも、Cに変えても変わらない」と思ってしまうのか、その理由を説明したいと思います。
スポンサーリンク
モンティホール問題を直感的に解くと間違えてしまう理由は?
(1)最後に残る箱は2つで、当たりはそのうちの1つ。だから1/2に決まってる!
普通に考えると、最後に残る箱は2つで、当たりはそのうちの1つ。
だから、どちらを選んでも、当たる確率は1/2に決まってる…というのが、直感的に考えると陥りやすい罠だと思います。
でも、最初は3択問題だった…この部分が重要なのです!
なんで、確率が変わるのか。
数学が得意な人なら、気づくかもしれません。
答えがAに入っている場合と、BもしくはCに入っている場合には、司会者が箱を一つ開けるという意味合いが大きく変わってくるためです。
例えば、Bに答えが入っている場合、司会者はBを開けることができないのです。
つまり、司会者はCを開けざるを得ないのです。
Aに答えが入っている場合は司会者はBもCも開ける権利がありますが、BかCに答えが入っている場合は司会者はどちらか片方の箱しか開けることができないのです。
ここが、確率を狂わせる要素となるわけです。
(2)でも、場合分けしたとしても、1/2のままじゃないか!
確率の問題の基本は、中学校でも学びますが、樹形図を書いてすべての場合分けをすることが基本になります。
で、数学が好きな人であれば、この問題を考えるときに、真っ先に場合分けをするのではないでしょうか。
では、この問題を場合分けしてみましょう!
この問題では樹形図の代わりに表で考えてみましょう。
【あなたがAを選んだときの場合分け】
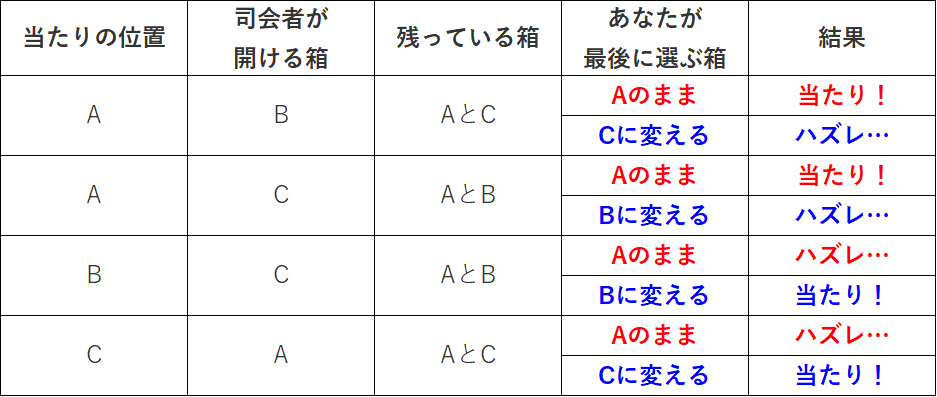
さて、あなたがAを選んだときの、すべての場合分けをしてみました。
そうすると、当たる確率をみてみると、Aのままを選んだ場合(上記表では赤字)も、BかCに変えた場合(上記表では青字)も、当たる確率が1/2だということが分かります。
場合分けは嘘をつかない…でも、ここにも実は罠が潜んでいます。
では、ここからは、できる限り簡単に解説をしていきたいと思います。
スポンサーリンク
モンティホール問題をできる限り簡単に解説します!
(1)場合分けのどこが間違っていたのか?
さて、先ほどの場合分けについて考えてみましょう。
実はこの問題、トリックがあるのです。
箱がA・B・C…といったように名付けられているため、3種類あると思ってしまうのです。
でも実は、箱は「当たりの箱」と「ハズレの箱」の2種類しかないのです。
つまり、A・B・Cの箱は、以下の図のように「当たりの箱」1つと「ハズレの箱」2つと言い換えられるわけです。
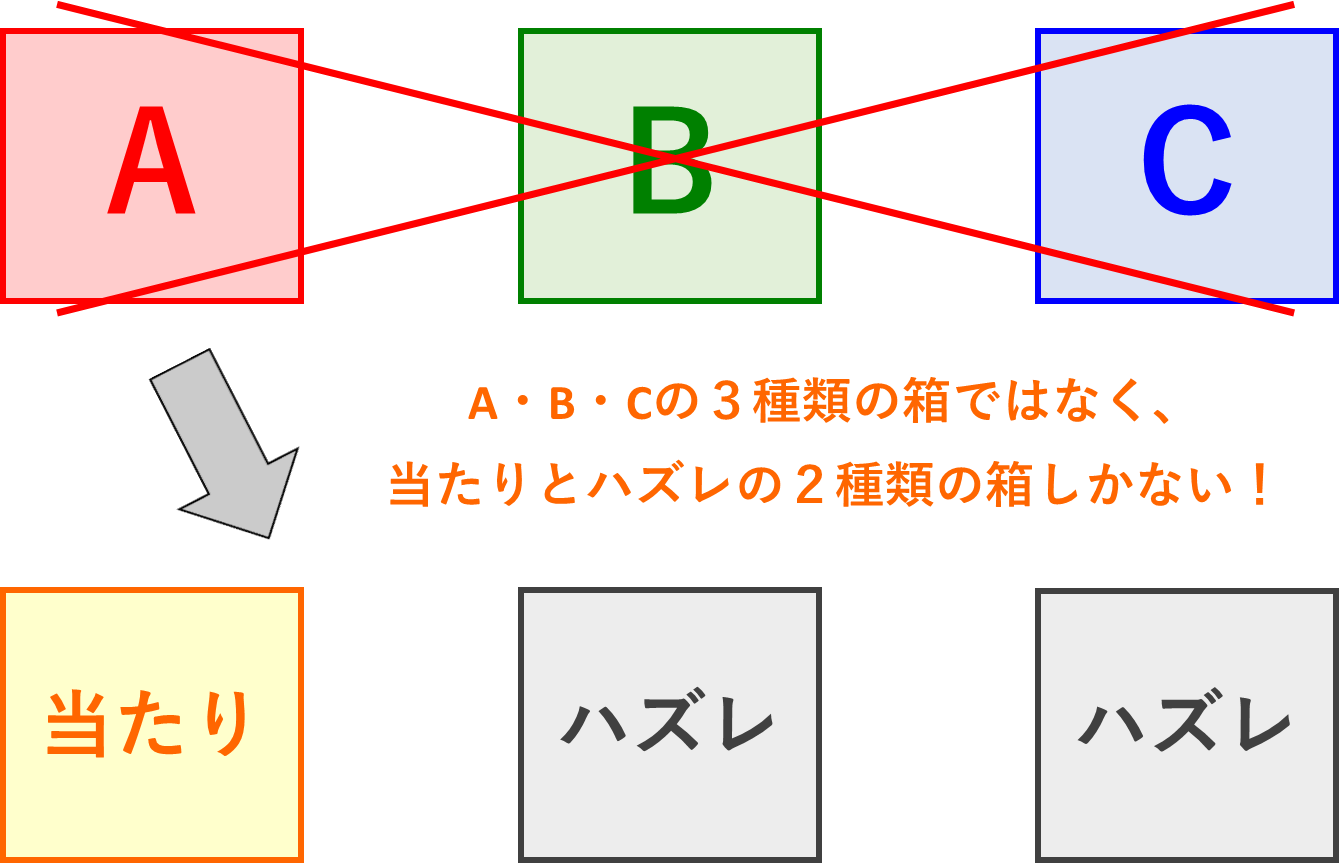
更に、A・B・Cそれぞれに、当たりが入っているパターンは以下の図のようになります!
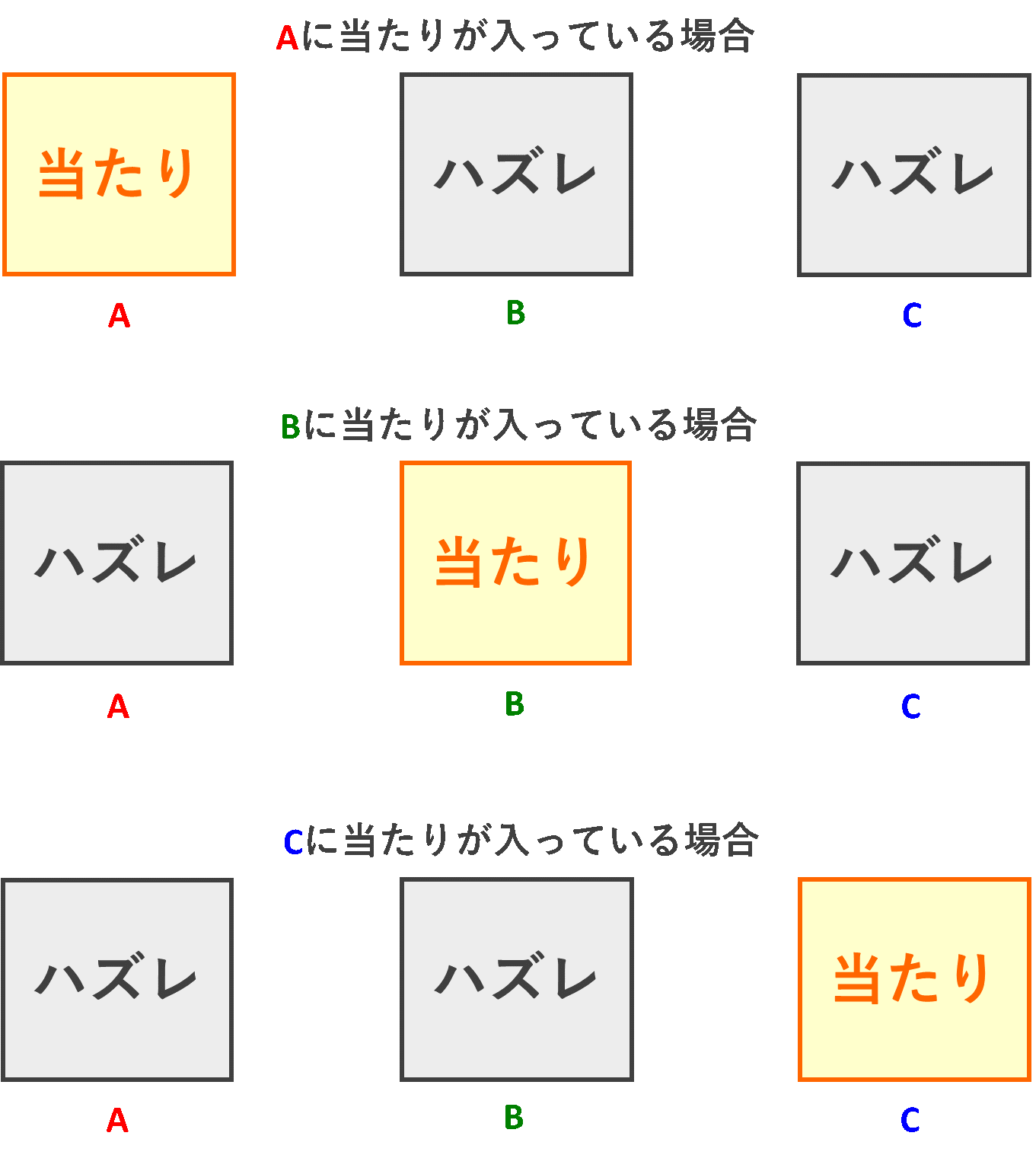
そして、最初にAを選び、Aが「当たりの箱」である場合、BとCは両方とも「ハズレの箱」と同じものであるため、以下の図のようにBとCという区別ができなくなるわけです!

さて、それを踏まえたうえで、はじめの表に戻りましょう。
【あなたがAを選んだときの場合分け】
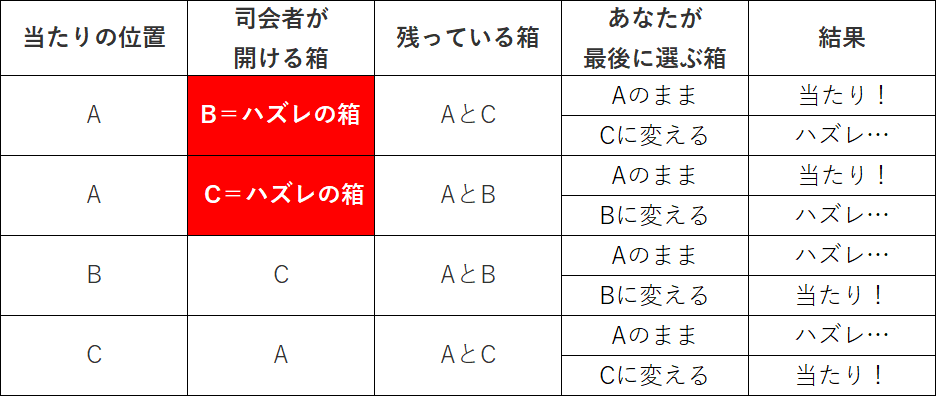
この場合分けの表を見てみると、上記の赤背景の部分がおかしいことになるのです。
BとCの両方とも、「ハズレの箱」という同じ箱なので、2通りのカウントをしてはいけないのです!
そのため、この場合分けの方法は間違っていたことになるのです。
(2)選択肢を「変える」・「変えない」に着目して確率を考える
様々なサイトで、モンティホール問題の解説がなされていますが、個人的に一番分かりやすく、納得できた解説を紹介します。
それは、選択肢を「変える」・「変えない」に着目して考えてみるのです。
また、表にしてみて考えましょう!
【あなたがAを選んだときの場合分け(選択肢を「変える」・「変えない」に着目した場合】
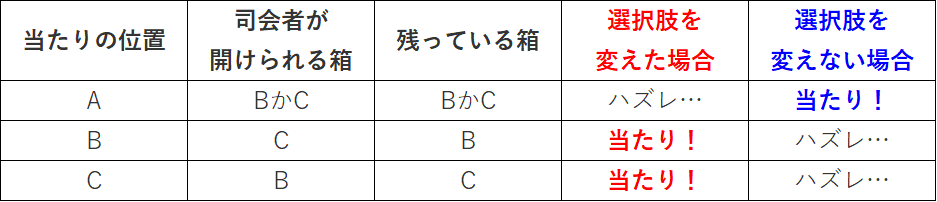
さて、このように考えると、真実が分かると思います。
あなたがAを選び、Aに当たりの位置があるとき、選択肢を変えた場合、絶対にハズレます。
一方で、あなたがAを選び、BもしくはCに当たりの位置があるとき、選択肢を変えた場合、絶対に当たります。
上記の表を縦に見てください。
選択肢を変えた場合(上記表では赤字)は、当たりの位置がAのときはハズレで、BとCのときは当たりなので、2/3で当たることとなります!
一方で、選択肢を変えなかった場合(上記表では青字)は、当たりの位置がAのときは当たりで、BとCのときはハズレなので、1/3で当たることとなります。
そう考えると、選択肢を変えた方が、当たる確率が高いという結論になるのです!
スポンサーリンク
おわりに

さて、今回の記事はいかがでしたでしょうか。
最近、思考実験に関する本がたくさん書店に並んでいますが、その中で紹介されており、面白いと思ったので記事にしてみました。
もちろん、私がこの問題をはじめに見たとき、「選択肢を変えても変えなくても、確率は一緒だろ!」と思っていたのですが、実際は違ったため、かなり衝撃を受けたのです。
で、解説を見たところ、最初は「なるほど!」と思ったのですが、考えれば考えるほど、解説自体に疑問を覚え始めてきたのです。
そのため、自分なりに納得するために、思考を重ねた結果、今回紹介した記事の解説に至ったわけです。
恐らく、「この問題を知っているけれども、解説を見ても理解できない…!」なんて人も多いのではないかと思います。
だからこそ、今回はできる限り、分かりやすく解説をしてみた次第です。
話は変わりますが、思考実験に関する本は、頭をフル回転させてくれるため、論理的思考力を鍛えるためにはもってこいだと思っています。
今回の問題を考えてみて疲れたという人もいると思いますが、確実に頭を鍛えることにつなげられたのではないでしょうか?
売れている本ではありますが、個人的に思考実験で面白かった本を紹介したいと思います。
そして、以前に、論理的思考(ロジカルシンキング)のトレーニング方法を記事にまとめましたので、興味がある方は以下のリンクからご覧ください!
理詰めな人に対抗するためのロジカルシンキングのトレーニング方法とは?
それでは、今回はこの辺で終えたいと思います。
もし、今回の記事が、少しでもお役に立てたのであれば、大変幸いです。
それでは、また次回も、よろしくお願いいたします!
コメント
この記事へのトラックバックはありません。














この記事へのコメントはありません。